Coeficiente Percentílico de Curtose: 3 Interpretações

A análise de dados estatísticos é uma etapa crucial em diversas áreas do conhecimento, sendo fundamental para a tomada de decisões baseadas em evidências. Um dos indicadores importantes na análise de distribuições de dados é o coeficiente percentílico de curtose. Este artigo explora o conceito, a importância e a aplicação desse coeficiente, fornecendo uma compreensão completa para iniciantes e profissionais da área.

O Que é Curtose?

Curtose é uma medida estatística que descreve a forma da distribuição de uma variável aleatória, especialmente a “altura” e a “largura” dos picos na distribuição dos dados. Seu cálculo envolve especialmente as medidas de dispersão dos dados. Basicamente, a curtose indica se os dados possuem caudas pesadas ou leves em relação a uma distribuição normal.

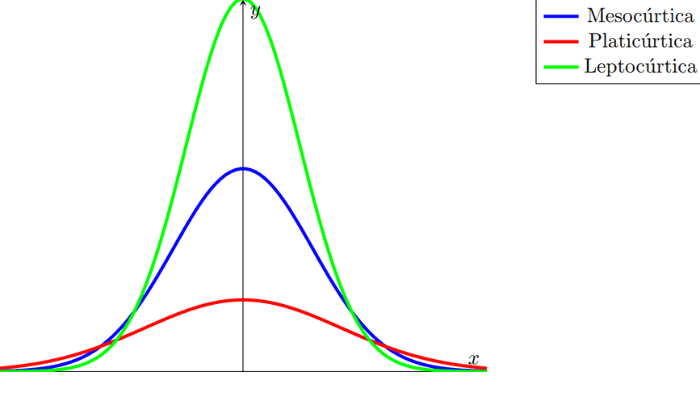
Existem três tipos de curtose:

• Mesocúrtica: Distribuição normal, com curtose igual a zero.
• Leptocúrtica: Distribuição com caudas mais pesadas e picos mais altos (curtose positiva).
• Platicúrtica: Distribuição com caudas mais leves e picos mais baixos (curtose negativa).

O Coeficiente Percentílico de Curtose

O coeficiente percentílico de curtose é uma variação do cálculo tradicional de curtose, utilizando percentis, combinados com a amplitude semi-interquartílica para medir a concentração dos dados. Esta amplitude é uma medida de dispersão que envolve os quartis: primeiro e terceiro quartis. Essa abordagem é menos sensível a outliers extremos e fornece uma perspectiva mais robusta da distribuição dos dados.

Fórmula do Coeficiente Percentílico de Curtose

Em primeiro lugar, a fórmula do coeficiente percentílico de curtose é dada por:

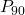• ​ é o percentil de ordem 90;
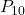• é o percentil de ordem 10;
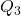• é o terceiro quartil;
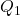• é o primeiro quartil.

Finalmente, essa fórmula compara a amplitude da faixa interpercentil mais ampla (P90 a P10) com a largura da distância semi-interquartil (metade da diferença entre Q1 a Q3). Sendo assim, valores maiores desse coeficiente indicam curvas leptocúrtica, enquanto valores menores indicam menor curtose e, portanto, curvas de frequências platicúrticas.

Interpretação do Coeficiente Percentílico de Curtose

Para realizar a interpretação do coeficiente percentílico de curtose devemos nos basear na distribuição gaussiana. A curtose indica até que ponto a curva de frequência de uma distribuição se apresenta mais afilada ou mais achatada do que uma curva padrão, denominada curva normal.

Interpretação

Do resultado da fórmula vamos obter um número adimensional, que vamos interpretar da seguinte forma:

• k = 0,263 indica que a curva de frequência ou a distribuição é mesocúrtica;
• k>0,263 curva ou distribuição platicúrtica;
• k<0,263 curva ou distribuição leptocúrtica.

Aplicações Práticas

As aplicações práticas do conhecimento das medidas de curtose vão desde finanças e econometria até ciências sociais e psicometria. Diversas áreas usam e empregam os conhecimentos e interpretações dessa medida de forma.

1. Finanças: No mercado financeiro, entender a curtose de retornos de ativos é crucial para avaliação de riscos. Ativos com alta curtose podem indicar maior probabilidade de retornos extremos.
2. Ciências Sociais: Em pesquisas sociais, pode ajudar a identificar distribuições atípicas de respostas em questionários, auxiliando na interpretação de comportamentos.
3. Engenharia: Utilizado na análise de variabilidade de processos, ajudando a identificar problemas de consistência na produção.

Além das aplicações acima, quando se trata de concurso público é importante ter em mente não apenas a fórmula, mas como interpretar e resolver rapidamente questões de concurso. Para isso é importante um curso e um treinamento especializado em estatística para concurso.

Ingresse agora no curso de estatística para concurso e dê o próximo passo para sua aprovação!

Conclusão

O coeficiente percentílico de curtose é uma ferramenta poderosa na análise de distribuições de dados, proporcionando insights valiosos sobre a forma e a dispersão dos dados. Ao utilizar percentis, oferece uma análise robusta e menos sensível a outliers, sendo útil em diversas áreas como finanças, ciências sociais e engenharia. Incorporar essa medida na análise estatística pode enriquecer a interpretação e a compreensão dos dados.