
A regressão linear simples é uma técnica estatística fundamental que permite entender a relação entre duas variáveis contínuas. Este artigo vai guiar você através de um passo a passo detalhado para compreender essa técnica essencial. Vamos abordar conceitos básicos, como interpretar os resultados e como aplicar a regressão linear simples em diferentes contextos.
Conteúdo
- 1 Passo 1: Compreendendo o Conceito de Regressão Linear Simples
- 2 Passo 2: Coleta e Preparação dos Dados
- 3 Passo 3: Plotando os Dados
- 4 Passo 4: Cálculo dos Coeficientes
- 5 Passo 5: Ajustando o Modelo de Regressão
- 6 Passo 6: Avaliação do Modelo
- 7 Passo 7: Uso de Software Estatístico
- 8 Passo 8: Interpretação e Comunicação dos Resultados
- 9 Conlusão
Passo 1: Compreendendo o Conceito de Regressão Linear Simples
A regressão linear simples é usada para modelar a relação entre uma variável dependente ![]() e uma variável independente
e uma variável independente ![]() . O objetivo é encontrar uma linha reta que melhor ajuste os dados, minimizando a distância entre os pontos de dados e a linha. A equação da linha é dada por:
. O objetivo é encontrar uma linha reta que melhor ajuste os dados, minimizando a distância entre os pontos de dados e a linha. A equação da linha é dada por:
![]()
Onde:
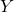 é a variável dependente;
é a variável dependente;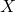 é a variável independente;
é a variável independente;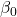 é o intercepto;
é o intercepto;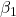 é o coeficiente angular;
é o coeficiente angular; é um termo de erro.
é um termo de erro.
DICA: Em verdade, para entender bem o que se passa na regressão linear simples, primeiramente você deve conhecer bem o modelo de distribuição normal de probabilidade, pois o pano de fundo é que a regressão é um refinamento desse modelo.
Quer aprender o essencial sobre a distribuição normal? Acesse o curso Distribuição Normal Essencial – curso rápido e prático para as probabilidades e aplicações desse modelo.
Passo 2: Coleta e Preparação dos Dados
Antes de realizar a regressão, é crucial coletar e preparar os dados adequadamente. Normalmente se dispõe de uma amostra de pontos do tipo ![]() , ou seja, uma amostra de dados bivariados. A preparação desses dados pode incluir:
, ou seja, uma amostra de dados bivariados. A preparação desses dados pode incluir:
- Garantir que os dados sejam contínuos e não categóricos.
- Verificar a ausência de valores ausentes (missing values) ou outliers extremos.
- Normalizar ou padronizar os dados, se necessário.
Quando se trata de resolver questão de concurso, o contexto é a resolução de uma prova escolar. Então se prepare bem para calcular somatórios e médias.
Passo 3: Plotando os Dados
Plotar os dados em um gráfico de dispersão é uma boa prática inicial. Isso ajuda a visualizar a relação entre ![]() e
e ![]() e a identificar possíveis padrões ou outliers.
e a identificar possíveis padrões ou outliers.
Além disso, um gráfico de dispersão pode nos ajudar a verificar a existência de correlação ou associação entre as variáveis
Passo 4: Cálculo dos Coeficientes
Os coeficientes ![]() (intercepto) e
(intercepto) e ![]() (inclinação) são calculados para minimizar a soma dos quadrados dos erros (diferença entre os valores observados e os valores obtidos na estimação). Os cálculos são realizados usando métodos estatísticos como o método dos mínimos quadrados.
(inclinação) são calculados para minimizar a soma dos quadrados dos erros (diferença entre os valores observados e os valores obtidos na estimação). Os cálculos são realizados usando métodos estatísticos como o método dos mínimos quadrados.

Em outras palavras, a teoria por traz desse procedimento é que admitimos que estamos cometendo um erro ao estimar a reta teórica pela reta obtida no cálculo dos coeficientes. Isso ocorre independente do método de estimação escolhido.
Por outro lado, o que se deseja é minimizar os erros que se cometem, usando algum princípio de otimização, como o de mínimos quadrados ordinários.
Passo 5: Ajustando o Modelo de Regressão
Com os coeficientes calculados, ajustamos o modelo de regressão linear. A equação final pode ser usada para prever valores de ![]() para dados novos de
para dados novos de ![]() .
.
Esse procedimento é usado tanto para entender a relação ou a associação entre as variáveis, como para realizar previsões.
O modelo de regressão linear simples tem muitas aplicações em diversas áreas do conhecimento:
- Econometria: Para analisar a relação entre variáveis econômicas, como o impacto da taxa de juros no investimento ou a relação entre inflação e desemprego.
- Finanças: Para prever preços de ações com base em variáveis como o índice de mercado ou volumes de negociação.
- Machine Learning: Utilizado em mercados financeiros para prever o preço futuro de ativos com base em variáveis econômicas e histórico de preços.
- Análise de Séries Temporais: Para prever valores futuros com base em dados históricos, como vendas mensais ou temperatura diária.
- Processamento de Linguagem Natural (NLP): Para prever a popularidade ou engajamento de um artigo com base em características textuais, como comprimento do texto ou frequência de palavras-chave.
- Otimização de Marketing Digital: Para prever o desempenho de campanhas de marketing digital, como cliques em anúncios ou conversões, com base em métricas como gasto em publicidade e número de impressões.
- Modelagem de Riscos: Para prever o risco de crédito ou probabilidade de inadimplência com base em características do solicitante, como histórico de crédito e renda.
- Sistemas de Recomendação: Para prever a preferência do usuário por determinados itens com base em seu histórico de interações e características dos itens.
- Engenharia de Software: Para prever o esforço necessário para concluir um projeto de software com base em variáveis como tamanho do projeto e experiência da equipe.
- Detecção de Anomalias: Para identificar comportamentos anômalos em sistemas, como detecção de fraudes em transações financeiras.
Passo 6: Avaliação do Modelo
Avaliar o modelo é essencial para entender sua precisão e eficácia. As principais métricas incluem:
- Coeficiente de Determinação (
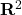 ): Indica a proporção da variabilidade de
): Indica a proporção da variabilidade de 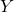 explicada por
explicada por 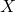 . Valores próximos a 1 indicam um bom ajuste.
. Valores próximos a 1 indicam um bom ajuste. - Erro Padrão dos Resíduos: Mede a precisão das previsões do modelo.
- p-valor dos Coeficientes: Testa a significância estatística dos coeficientes.
É importante que os pressupostos do modelo de regressão linear simples confirmem o modelo teórico por trás da associação entre as variáveis. Para este objetivo é sempre importante trabalhar em conjunto com profissionais de outras áreas como, por exemplo, economia, psicólogos, profissionais do marketing etc.
Passo 7: Verificação dos Pressupostos
Para que os resultados da regressão sejam válidos, alguns pressupostos devem ser verificados:
- Linearidade: A relação entre
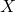 e
e 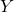 deve ser linear nos parâmetros.
deve ser linear nos parâmetros. - Homocedasticidade: A variância dos resíduos deve ser constante.
- Normalidade dos Resíduos: Os resíduos devem seguir uma distribuição normal.
- Independência dos Erros: Os resíduos devem ser independentes entre si.
A regressão linear simples é uma ferramenta estatística muito aplicada no dia-a-dia, mas sua validade depende da confirmação dos pressupostos teóricos tanto da estatística quanto da teoria envolvendo a relação que se quer validar.
Passo 7: Uso de Software Estatístico
Ferramentas como Excel, R, Python (com bibliotecas como pandas e statsmodels) e SPSS podem facilitar a realização de regressões lineares, assim sendo, no mundo real das aplicações será importante conhecer e usar um software estatístico. No contexto de estatística e ciência de dados R e Python são os queridinhos da comunidade.
Por outro lado, no mundo dos concursos, você será exigido a calcular, interpretar e comunicar os resultados do modelo de regressão linear simples.
Passo 8: Interpretação e Comunicação dos Resultados
Após ajustar e avaliar o modelo, é importante interpretar e comunicar os resultados de forma clara. Explique o significado dos coeficientes, a precisão do modelo e suas limitações.
Apesar da regressão indicar uma relação estatística bem ajustada, pode ser que a teoria por traz do fenômeno estudado não seja coerente com o modelo de regressão linear simples. Nesse ponto é importante ter prudência para não chegar a conclusões errôneas por meio do modelo ajustado.
Curso de Estatística para Concurso: o mais completo para aprovação em estatística e probabilidade.
Conlusão
A regressão linear simples é uma ferramenta poderosa para análise de dados e previsão. Seguindo estes passos, você pode entender e aplicar essa técnica em diversas situações, melhorando suas habilidades analíticas.
Em que pese o modelo estatístico possa ser calculado e ajustado facilmente por um software estatístico, é necessário prudência na interpretação e comunicação dos resultados.
Regressão linear simples: use com moderação.







Deixe um comentário