A Distribuição Uniforme de Probabilidades

Vamos aprender algumas características da distribuição uniforme para ajudar você em concursos.

Nessa postagem vamos conhecer a distribuição uniforme de probabilidades. Este modelo teórico de distribuição contínua é um dos mais simples dentro do campo de probabilidade e estatística. Apesar de sua simplicidade, nem sempre apresenta cálculos simples quando o assunto é uma prova de concurso. Entretanto a distribuição uniforme é extremamente útil para aprendermos alguns cálculos de probabilidade.

Se você precisa aprofundar conhecimentos de probabilidade para realizar uma prova de concurso em alto nível, convido você a aprender mais sobre distribuições de probabilidade nas próximas linhas. Leia até o final e eleve o nível da sua preparação para concurso público.

Conteúdo

1 Função de Densidade da Distribuição Uniforme.
- 1.1 Outras Funções Importantes
2 Função de Distribuição Acumulada
3 Parâmetros da Distribuição Uniforme
4 Conclusão

Função de Densidade da Distribuição Uniforme.

As variáveis aleatórias se subdividem basicamente em duas categorias: contínuas e discretas. A distribuição uniforme se enquadra dentro do primeiro grupo, por isso mesmo ela é caracterizada por uma função densidade de probabilidade.

Em primeiro lugar, a identidade de uma variável aleatória contínua é a sua função densidade de probabilidade. Abaixo consideramos uma distribuição que assume valores entre 0 e 1. A expressão da densidade é dada por:

$\[f(x)=\begin{cases}1,\ \mbox{se}\ 0\leq x\leq 1\\ 0,\ \mbox{caso contrário}$

Partindo da função de densidade, vamos destacar duas informações:

A parte útil: 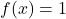$f(x)= 1$ é essa expressão que vamos usar para os diversos cálculos;
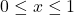$0\leq x\leq 1$ : isso significa que essa variável aleatória assume valores apenas no intervalo de 0 a 1.

Uma observação importante para nossos cálculos é que é indiferente usar um intervalo aberto ou fechado, já que as variáveis aleatórias contínuas assumem probabilidade nula no ponto.

Outras Funções Importantes

Em probabilidade temos outras funções importantes para caracterizar as distribuições de maneira geral. São elas:

A função geradora de momentos; e
A função característica.

Assim como reconhecemos um indivíduo pelo seu registro geral – RG ou CPF ou CNH – assim temos algumas maneiras distintas de identificar um modelo de probabilidade.

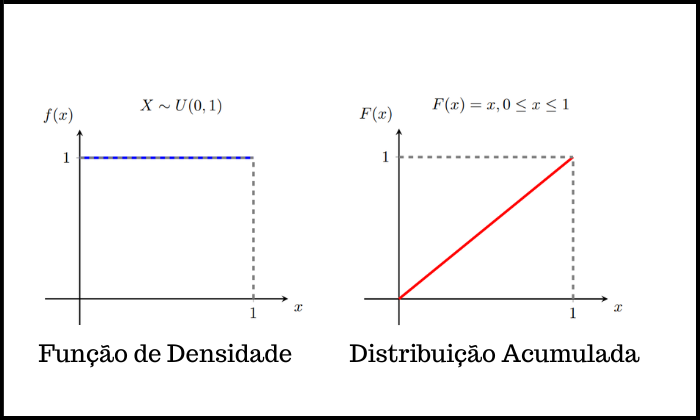
Função de Distribuição Acumulada

Para calcular a probabilidade numa distribuição uniforme o procedimento é resolver uma integral simples. Nosso objetivo aqui é mostrar que cálculos de probabilidade envolvendo integrais podem ser mais simples do que se imagina.

$P(X\leq x)= \int_0^xf(t)\ \mathrm{d}t = t\big|_0^x = x,\ 0\leq x \leq 1$

Em resumo, podemos escrever: $F(x)=x,\ 0\leq x\leq 1$ . Ou seja a probabilidade de que a distribuição uniforme assuma um valor menor ou iguala $x$ é o próprio valor $x$ .

Função de densidade e de distribuição acumulada

Parâmetros da Distribuição Uniforme

Em probabilidade e estatística frequentemente teremos de calcular alguns parâmetros das distribuições mais comuns. Para calcular a média e a variância da distribuição uniforme procedemos da seguinte maneira.

Valor Esperado

O valor esperado é definido por uma integral aplicada sobre a multiplicação de x pela sua função de densidade.

$\begin{align*}\mathbb{E}(X)&=\int_0^1x\cdot f(x)\mathrm{d}x\\ \mathbb{E}(X)&=\int_0^1 x \mathrm{d}x\\ \mathbb{E}(X)&=\frac{x}{2}\Big|_0^1\\ \mathbb{E}(X)&=\frac{1}{2}\\ \end{align*}$

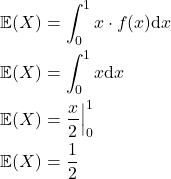
Variância

Para calcular a variância podemos seguir a definição geral:

$\begin{align*}\mathbb{V}(X)&=\int_0^1(x-\mathbb{E}(X))^2\cdot f(x)\mathrm{d}x \end{align*}$

Outra maneira alternativa de realizar esse cálculo é por meio da fórmula $\mathbb{V}(X)=\mathbb{E}(X^2)-\mathbb{E}(X)^2$ , Obtemos a primeira parcela de modo semelhante ao cálculo do valor esperado:

$\begin{align*}\mathbb{E}(X^2)&=\int_0^1x^2\cdot f(x)\mathrm{d}x\\ \mathbb{E}(X^2)&=\int_0^1 x^2 \mathrm{d}x\\ \mathbb{E}(X^2)&=\frac{x^3}{3}\Big|_0^1\\ \mathbb{E}(X^2)&=\frac{1}{3}\\ \end{align*}$

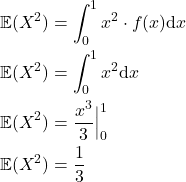
Agora fazemos:

$\begin{align*}\mathbb{V}(X)&=\mathbb{E}(X^2)-\mathbb{E}(X)^2\\ \mathbb{V}(X)&=\frac{1}{3}-\frac{1}{4}=\frac{1}{12} \end{align*}$

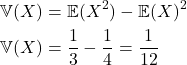
Cálculo do Desvio Padrão

O desvio padrão, assim como a variância são parâmetros importantes para a distribuição uniforme. Conforme a formulação geral, para obtê-lo devemos calcular a raiz quadrada da variância.

$\mathbb{D}(X)=\sqrt{\mathbb{V}(X)}=\frac{1}{\sqrt{12}}$

Coeficiente de Variação

Outra importante medida de variabilidade é o coeficiente de variação. Por meio dessa medida é possível realizar comparações entre diferentes conjuntos de dados quanto à variabilidade dos mesmos. Temos a seguinte fórmula:

$\hbox{Cv}(X)=\frac{ \mathbb{D} }{\mathbb{E}(X)}$

$\hbox{Cv}(X)=\frac{ 1/\sqrt{12} }{1/2}=\frac{1}{2\sqrt{12}}$

Caso um conjunto de dados possua maior coeficiente de variação em relação a outro podemos realizar a comparação direta das variabilidades relativas para decidir qual desse conjuntos de dados seria mais dispoerso.

Conclusão

Nesse artigo mostramos para você as principais características da distribuição uniforme. Por meio de cálculos e definições vimos os principais parâmetros de interesse na distribuição uniforme do tipo 0 e 1. Esses cálculos nos ajudam a entender como usar integrais conjugadas com as definições dos parâmetros de interesse em probabilidade.

Se você vai fazer um concurso com probabilidade e estatística e precisa entender e aplicar conceitos importantes como integrais e derivadas, conheça o curso Matemática Essencial para Concursos: um curso rápido e prático, direto ao ponto para você aprender e aplicar os conceitos matemáticos em probabilidade e estatística!

Os melhores cursos de estatística para concursos: