Assimetria: 3 formas das curvas de frequências

Em estatística, a assimetria diz respeito à forma de uma curva de frequência. Também pode se referir à medida associada à forma de uma função densidade de probabilidade ou de uma função de probabilidade.

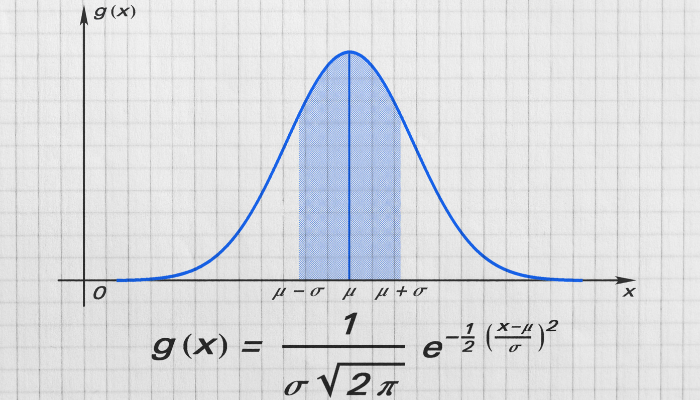
Assimetria também pode se referir à falta de simetria de uma distribuição de frequência. Uma distribuição é simétrica quando a média, a mediana e a moda coincidem. Quando a distribuição é assimétrica, um dos valores de média, mediana ou moda está mais afastado dos outros dois.

Assimetria Positiva

A assimetria positiva ou à direita refere-se ao padrão das curvas de frequência que possuem uma calda mais alongada no sentido positivo do eixo dos x.

Essa medida positiva fica evidenciada quando a cauda direita da distribuição é mais longa que a cauda esquerda. Nesse caso, a média é maior que a mediana e a moda.

Assimetria negativa

Ocorre a assimetria à esquerda ou negativa quando a cauda esquerda da distribuição é mais longa que a cauda direita. Nesse caso, a média é menor que a mediana e a moda.

Existem várias formas de se verificar a forma de uma distribuição de frequências, como por exemplo dispositivos gráficos, medidas envolvendo momentos ou ainda coeficientes.

Método gráfico

Para verificar a forma da uma curva, podemos fazê-lo usando um método gráfico. Você pode empregar a visualização da forma dos dados por meio de:

• Histograma;
• Box-plot;
• Ramo-e-folhas;
• Gráfico de quantis.

Esses gráficos podem revelar o padrão e a forma dos dados.

Algumas medidas e coeficientes

Por meio da medida de coeficientes de assimetria podemos determinar a forma das curvas de frequências, portanto, para isso podemos usar:

• Primeiro coeficiente de Pearson;
• Segundo coeficiente de Pearson;
• Dispersão inferior e dispersão superior;
• Esquema de cinco números;
• Relação empírica entre média, moda e mediana;
• Coeficiente quartílico;

Conclusão

Para concluir pela assimetria você deve combinar os métodos gráficos com os métodos numéricos envolvendo algum ou alguns dos coeficientes apresentados.

O estudo desse tema está inserido dentro da estatística descritiva, embora possa envolver alguns aspectos dentro do estudo de probabilidade e também de momentos de uma distribuição.