Concurso Câmara Federal Prova de Estatística

Se você fez o Concurso Câmara Federal é hora de conferir a resolução da prova de estatística. Vamos mostrar para você a resolução completa das 8 questões dessa disciplina. Mais do que nunca é hora de conferir se todo o seu esforço foi recompensado. Acompanhe abaixo cada uma das resoluções das questões.

Ao final trazemos algumas dicas adicionais para você que precisa se preparar em alto nível para um concurso com um programa de estatística e probabilidade.

Conteúdo

1 Analista Legislativo
2 Técnico em Material e Patrimônio
3 Conclusão

Analista Legislativo

O concurso Câmara Federal trouxe diversas oportunidades subdivididas em várias especialidades. Para quem concorreu às vagas de Analista Legislativo – Técnico em Material e Patrimônio, além de um vasto programa de conhecimentos específicos foi exigida uma prova de estatística.

Ao todo foram 8 questões que versavam acerca de probabilidade e estatística. Foi uma prova bem tradicional ao estilo FGV, mas sem surpresas.

Baixe agora uma coletânea de provas FGV de estatística resolvidas na íntegra. Veja mais provas de estatística.

Técnico em Material e Patrimônio

A prova para Analista Legislativo Técnico em Material e Patrimônio no Concurso Câmara Federal teve a seguinte distribuição de assuntos do conteúdo programático:

Probabilidade (2): distribuições binomial e normal – 1 questão de cada;
Medidas de posição e quartis (2): 1 questão sobre média amostral; outra sobre outliers (quartis);
Medidas de dispersão (1): cálculo de variância;
Análise de regressão linear (1): versava sobre coeficiente de correlação;
Estimação de parâmetros (1): máxima verossimilhança, tendenciosidade de um estimador (vício);
Distribuições de probabilidade (1): Cálculo de valor esperado pela função de probabildidade.

A prova do Concurso Câmara Federal, de maneira geral, foi bem tranquila sem questões obscuras ou duvidosas.

Além disso, sequer foi exigido muito cálculo na prova. Bastava um pouco mais de sagacidade para uma resolução rápida das questões.

Confira abaixo as questões no detalhe:

Média

A primeira questão de estatística do concurso câmara federal versava sobre a média. Uma questão bem previsível.

63. A média de um conjunto de 18 salários mensais de uma empresa de desenvolvimento era R$5.500,00. Recentemente, dois novos funcionários foram incorporados, um com salário mensal de
R$6.000,00, outro com salário mensal de R$6.800,00. Assim, a nova média salarial mensal passou a ser de

(A) R$5.550,00
(B) R$5.590,00
(C) R$5.650,00
(D) R$5.700,00
(E) R$5.810,00

$\overline{x}_1=\frac{\displaystyle\sum_{i=1}^{18}x_i}{18}\Rightarrow \sum_{i=1}^{18}x_i = 18\times 5.509$

$\overline{x}_2=\frac{\displaystyle\sum_{i=1}^{18}x_i+6.000+6.800}{20}= \frac{111.800}{20}$

$\overline{x}_2=\text{R}\$\ 5.590,00$

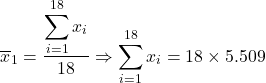
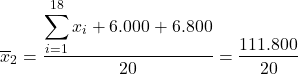
Gabarito: B

Cálculo de Variância

64. Observe a seguinte amostra de notas de cinco alunos:
6, 6, 8, 10, 10.
A variância dessas notas, entendida como a média dos quadrados
dos desvios em torno da média, é igual a
(A) 2,4.
(B) 2,8.
(C) 3,2.
(D) 3,6.
(E) 4,0.

Note que a distribuição de dados é perfeitamente simétrica, portanto a média é igual à mediana, que corresponde à observação central. Portanto igual a 8.

$(6-8)^2$	4
$(6-8)^2$	4
$(8-8)^2$	0
$(10-8)^2$	4
$(10-8)^2$	4
Soma	16

A variância é dada por

$\sigma^2=\frac{\displaystyle\sum_{i=1}^{5}(x_i-\overline{x})^2}{5}=\frac{16}{5}=3,2$

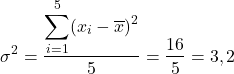
Gabarito: C

Veja os melhores cursos de estatística para concurso:

Questão envolvendo quartis

65. Os dados a seguir são uma amostra de 40 idades:

7 18 20 20 20 21 21 24 25 26
26 28 28 29 30 32 34 34 36 36
36 36 37 37 38 38 38 39 40 40
40 41 41 43 48 48 49 50 50 59

Para a detecção de observações atípicas (outliers), será usado o critério que considera atípica a observação que não está no intervalo (Q1 – 1,5D; Q3 + 1,5D), em que D é a distância interquartil, Q1 é o 1º quartil e Q3, o terceiro. Assim, a quantidade de outliers com base nesse critério, para esse conjunto de dados, é igual a

(A) 0.
(B) 1.
(C) 2.
(D) 3.
(E) 4.

Para obter os quartis: primeiro e terceiro quartis, fazemos o seguinte cálculo:

$Q_1=\frac{x_{(10)}+x_{(11)} }{2}=\frac{26+26}{2}=26$

O terceiro quartil deve calcular a média entre as trigésima e trigésima primeira observações:

$Q_3=\frac{x_{(30)}+x_{(31)}}{2}=\frac{40+40}{2}=40$

Com isso obtemos a distância interquartílica

$D=Q_3-Q_1=40-16=14$

Assim o intervalo obtido é igual a $(Q_1-1,5D;Q_3+1,5D) =(5;61)$ . Portanto não há valores outliers, pois todo o conjunto de dados está dentro desse intervalo.

Gabarito: A

Correlação no concurso Câmara Federal

66. Avalie se as seguintes afirmativas acerca do coeficiente de correlação linear $\rho$ entre duas variáveis aleatórias contínuas estão corretas.

I. O módulo de $\rho$ é sempre menor ou igual a 1.
II. Se $\rho=0$ , as duas variáveis são independentes.
III. Valores de $\rho$ próximos de +1 indicam uma correlação positiva forte. Está correto o que se afirma em

(A) I, apenas.
(B) II, apenas.
(C) I e II, apenas.
(D) I e III, apenas.
(E) II e III, apenas.

Veja que as afirmações corretas são I e III. Para a correlação nula, vemos que $\rho=0$ é condição necessária, por outro lado duas variáveis independentes é condição suficiente para constatar a independência entre as duas variáveis. Portanto II é um item incorreto.

Finalmente podemos afirmar sem medo que se duas variáveis são independentes, então $\rho=0$ .

Gabarito: D

Distribuição Binomial

67. Numa população, 50% dos indivíduos já contraíram covid-19. Se uma amostra aleatória simples de 10 indivíduos for obtida dessa
população, a probabilidade de que 6 tenham contraído covid-19 é aproximadamente igual a
(A) 0,02.
(B) 0,05.
(C) 0,08.
(D) 0,10.
(E) 0,20.

A função de probabilidade binomial é dada por

$P(X=x)=\binom{10}{x}(1/2)^x(1/2)^{10-x},\$

Temos X assumindo valores de 1 a 10. Logo,

$P(X=x)=\binom{10}{6}(1/2)^6(1/2)^{4}$

$P(X=x)=\frac{105}{512}\approx 0,20$

Gabarito: E

Distribuição Normal

68. Se X é uma variável aleatória normalmente distribuída, com média 50 e variância 100, então a seguinte variável tem distribuição normal padrão:
(A) Z = (X – 50)/10.
(B) Z = (X – 50)/100.
(C) Z = (X + 50)/10.
(D) Z = (X + 50)/100.
(E) Z = X – 5

Quando uma variável aleatória X segue um modelo de distribuição normal, processo de padronização garante que

$\frac{X-\mu}{\sigma} \sim N(0,1)$

Concluímos essa questão com o resultado

$\frac{X-50}{\sqrt{100}}=\frac{X-50}{10} \sim N(0,1)$

Gabarito: A

Inferência: propriedades dos estimadores

69. Uma amostra aleatória simples $X_1, X_2, \ldots X_n$ de uma população
descrita por uma variável aleatória com distribuição normal de parâmetros $\mu$ e $\sigma^2$ desconhecidos será observada. Nesse caso, avalie se as seguintes afirmativas estão corretas:

I. A média amostral $\overline{X}$ é estimador não tendencioso de $\mu$ .
II. A média amostral $\overline{X}$ é estimador de máxima verossimilhança
de $\mu$ .
III. Um estimador não tendencioso de $\sigma^2$ é dado por
$\sum_{i=1}^{n}(X_i-\overline{X})^2}/n$ .

Está correto o que se afirma em
(A) I, apenas.
(B) I e II, apenas.
(C) I e III, apenas.
(D) II e III, apenas.
(E) I, II e III.

Nessa questão apenas o item III não é correto, pois o estimador não tendencioso para estimar $\sigma^2$ é $\frac{\displaystyle\sum_{i=1}^{2}(X_i-\overline{X})^2}{n-1}$

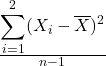
Gabarito: B (diverge do gabarito oficial preliminar).

Distribuição de Probabilidade

70. A função de probabilidade de uma variável aleatória discreta X é
dada por:

x	0	1	2	3
p(x)	0,2	0,3	0,3	0,2

Nesse caso, a variância de X é igual a
(A) 1,05.
(B) 1,15.
(C) 1,25.
(D) 1,35.
(E) 1,45

Vamos calcular a variância pela fórmula

$\sigma^2=\hbox{E}(X^2)-\hbox{E}(X)^2$

Temos $\hbox{E}(X)=0\times 0,2+1\times 0,3+2\times 0,3+3\times 0,2=1,5$

O segundo momento é dado por $\hbox{E}(X)=0^2\times 0,2+1^2\times 0,3+2^2\times 0,3+3^2\times 0,2=3,3$

Por fim, a variância é dada por

$\sigma^2=\hbox{E}(X^2)-\hbox{E}(X)^2=3,3-2,25=1,05$

Gabarito: A (diverge do gabarito oficial preliminar)

Veja a resolução no canal de estatística para concurso!

Gabarito Oficial Concurso Câmara dos Deputados

A banca FGV divulgou o gabarito oficial preliminar abaixo reproduzido:

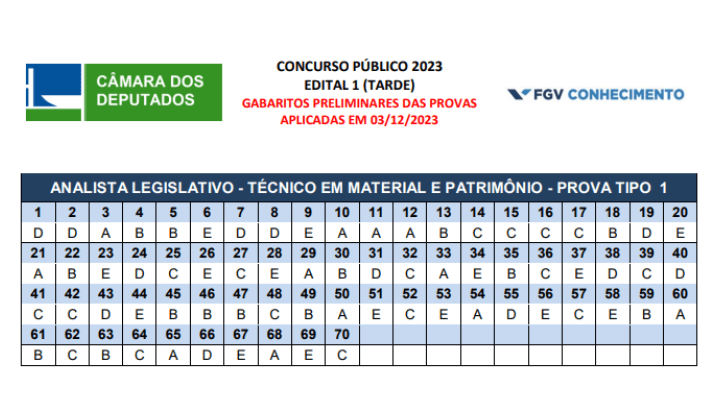
Concurso Câmara Federal - Gabarito Oficial Preliminar

De acordo com o gabarito acima, temos dois possíveis recursos para a prova de estatística da Câmara dos Deputados: questões 69 e 70.

Conclusão

A prova do concurso Câmara Federal para analista legislativo na especialidade Técnico em Material e Patrimônio veio bem tradicional.

Para quem estudou sem medo, a prova não surpreendeu muito. As questões vieram bem dentro do programa de estatística e se repetiu um padrão da FGV para uma prova que não foi aplicada especificamente para estatísticos.

Para quem não foi muito bem, temos uma dica adicional. Você pode ingressar no curso de estatística para concurso.

Muito boa sorte!

Concurso Câmara Federal Prova de Estatística – Resolução

Junte-se à lista Vip! Receba conteúdos exclusivos do mundo de estatística para concurso.

Compartilhe agora mesmo:

Analista Legislativo

Técnico em Material e Patrimônio

Média

Cálculo de Variância

Questão envolvendo quartis

Correlação no concurso Câmara Federal

Distribuição Binomial

Distribuição Normal

Inferência: propriedades dos estimadores

Distribuição de Probabilidade

Gabarito Oficial Concurso Câmara dos Deputados

Conclusão

Compartilhe agora mesmo:

Kaggle: O que É e Como Funciona – 3 Dicas

Concurso TRT CE: Estatística

Probabilidade de Ganhar na Loteria com 1 bilhete simples

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade