Em estatística, temos diversas maneiras de estimar a média: nesse artigo vamos conhecer o estimador de regressão. Uma das maneiras mais eficientes de estimar uma média de uma variável é por meio de uma informação de uma variável auxiliar. É exatamente isso que fazemos quando usamos essa técnica.
Leia até o final e saiba como usar o estimador de regressão, sua fórmula, pressupostos por trás do modelo, e muito mais para aprender um pouquinho mais acerca de técnicas de amostragem.
Conteúdo
Estimador de Regressão: Contexto
Quando usamos o estimador de regressão é importante não confundir com os estimadores de mínimos quadrados ordinários (MQO) ou os estimadores de máxima verossimilhança (EMV), comumente estudados em inferência estatística.
Para estimar os estimadores MQO e EMV ou mesmo estimadores do tipo BLUE (Best Linear Umbiased Estimator) recorremos a uma amostra de pares do tipo 
.
A diferença entre os métodos acima e os estimador do tipo regressão é que este último vai levar em consideração uma informação conhecida para a variável 
na população. Ou seja: além da amostra, temos um censo realizado sobre a variável .
Fórmula
Considerando o que vimos até aqui, a formulação do estimador de regressão para a média da população será a seguinte:
Onde:
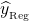denota o estimador de regressão;
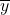é a média de 
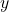na amostra;
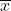é a média de 
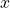na amostra;
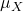é a média de 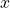na população.
É importante dizer que a informação acerca de na população faz toda a diferença em relação às técnicas de estimação comumente estudadas no contexto da estatística inferencial.
Faça download de provas de estatística para concurso.
Como obter o coeficiente b
Para saber como obter o coeficiente 
é necessário levar em conta duas abordagens para a estimação.
Primeiro consideramos que o coeficiente é um valor fixo 
, dessa forma não vamos usar a amostra para calcular uma estimativa desse coeficiente.
Em segundo lugar, podemos considerar a amostra para obter um estimador para esse coeficiente. Para isso devemos assumir algumas premissas básicas para obter esse estimador.
Por fim, podemos calcular usando a seguinte formula
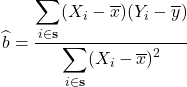
Veja como obter os estimadores de mínimos quadrados ordinários.
Informação da população
Comumente a informação da população é conhecido como a média populacional da variável . Nesse ponto o estimador de regressão se diferencia dos estimadores EMV ou MQO, pois estes se fiam inteiramente na amostra.
Lembre-se de que o objetivo de usar uma informação auxiliar é obter uma maior eficiência do estimador, assim obtemos um menor erro padrão do estimador.
Usamos os estimadores do tipo regressão por questões operacionais. Assim como no estimador de razão pode ser que conheçamos o tamanho da população N, mas não podemos obter todas as informações de 
, enquanto pode ser obtida mais facilmente.
Intuição
A intuição nos mostra que a medida que se aumenta o tamanho da população, mais próximo se chega do verdadeiro valor do parâmetro.
Ao observar a fórmula do estimador de regressão é exatamente isso que ocorre, pois sabemos que a média de é naturalmente o estimador não enviesado para média populacional. Como a diferença 
tende a se anular a medida que o tamanho da amostra cresce, naturalmente o estimador da média populacional se torna a média amostral.
Assim podemos ratificar que, de fato, a informação auxiliar é útil, quando não se pode obter facilmente as inferências para a variável resposta, em que pese ter disponível uma informação auxiliar de .
Por fim, é importante saber como estimar a variância do estimador de razão, assim como saber os pressupostos desse processo.
Deixe um comentário