Um dos principais tópicos para você estudar em concurso trata-se de inferência estatística. Nesse post vamos trazer dicas muito relevantes para sua prova de estatística.
Enquanto a parte descritiva da estatística se volta para o resumo de dados, a inferência indutiva, por outro lado, lida com estimação e teste de hipóteses.
Se você está se estudando estatística para concurso, vale a pena ler esse artigo até o final. Além de dicas de estudo você terá uma visão geral dessa matéria.
Conteúdo
A Inferência Estatística
O primeiro passo para entender inferência estatística é saber que ela se realiza a partir de uma amostra. Assim, por meio das técnicas inferenciais, buscamos extrapolar para o todo, aquilo que se estuda num subgrupo da população.
O principal objetivo é trabalhar com um conjunto de dados reduzido, tendo em vista que não á barato investigar o todo.
Dessa forma, faz-se necessário entender o quão reduzido devem ser os dados para que as conclusões sejam válidas.
Quando investigamos toda a população estamos realizando o que se chama de censo. Isso nem sempre é possível ou envolve altos custos operacionais.
Vamos trazer abaixo algumas dicas de estudo.
Como Estudar Estatística Inferencial
Por ser um assunto central dentro de estatística, a inferência requer muito conhecimento prévio da matéria. Ela se subdivide nos seguintes tópicos.
- Amostragem;
- Estimação pontual e intervalar;
- Propriedade dos Estimadores; e
- Teste de hipóteses.
Partindo dessa subdivisão deve se ter um conhecimento muito sólido em probabilidade, mas não só isso.
Primeiro de tudo, você deve ter em mente que tudo isso é matemática, portanto não deve ignorar essa base sob pena de se frustrar nos estudos.
Procure resolver bem equações de primeiro e segundo graus e tenha muito traquejo algébrico. Manipular expressões deve estar no sangue do concurseiro.
Ainda que você não tenha dificuldade em matemática básica, faça muitos exercícios para ficar na massa do sangue. É sério, NÃO SUBESTIME isso!
Saiba Usar As Tabelas de Probabilidade
Para se dar bem em inferência, você deve saber calcular quantis dos principais modelos por meio de uma tabela de probabilidade.
Em princípio saber calcular uma probabiilidade já é um bom caminho andado, mas não basta saber isso, é necessário saber identificar bem os quantis da distribuição em questão.
Uma vez que você sabe obter um quantil da distribuição normal, veja como obtê-los na qui-quadrado, t de student e distribuição F de Snedecor.
Por exemplo, 
diz respeito ao quantil da ordem 97,5% da distribuição normal padrão, por outro lado, considerando a simetria da distribuição normal, 
é o quantil de ordem 2,5%.
Em geral só esse conhecimento já ajuda você a ganhar tempo nas questões.
Conheça Bem as Propriedades da Média e Variância
Se pudesse dar uma ordem de importância, saber manipular médias e variâncias teria grau máximo de importância nos seus estudos.
Em que pese, tudo ser muito concatenado, apenas saber as propriedades de valor esperado pode garantir algumas questões de provas de concurso.
Assim, faça a revisão de combinação linear de variáveis aleatórias, logo em seguida, aplique essas propriedades, sério, vai facilitar muito os estudos.
A fim de trazer um exemplo pra você, veja a vídeo-aula abaixo para aprender trabalhar com médias e variâncias:
População e Amostra
Para entender inferência estatística aqui vou deixar um hack que pouca gente ensina, mas é de fundamental importância.
Uma população é uma função de densidade ou uma função de probabilidade. A partir dela vamos estimar parâmetros.
Uma população é uma função de densidade ou uma função de probabilidade.
Partindo desse ponto, parâmetro é um número real, portanto constante, entretanto é um valor desconhecido.
A amostra é um conjunto de dados, os quais consideramos uma réplica do modelo de probabilidade em estudo.
Por exemplo, considere uma amostra 
onda cada unidade 
é proveniente da distribuição binomial:
![\[ P(X_i=x_i)=\binom{n}{x_i}p^{x_i}(1-p)^{n-x_i}, x_i=1, 2, \ldots, n\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-f89dbac9bb7c2793faf827541db392fc_l3.png "Rendered by QuickLaTeX.com")
Como você vê cada réplica carrega a mesma característica da distribuição binomial com o mesmo parâmetro 
que vamos estimar.
Por fim, o que deve ficar claro é o aspecto matemático da inferência estatística, mas não aplicação prática na vida real.
Não se preocupe com as aplicações; pelo menos não se preocupe para o seu concurso.
Você deve lembrar que o ambiente de concurso é o acadêmico, portanto tradicionalmente você vai resolver uma prova escolar.
É uma perda de tempo frases do tipo: “onde vou usar isso”. Os melhores concurseiros hackeiam suas mentes para jogar o jogo do concurso como ele é.
Finalmente, entenda que esse é um modelo de estatística clássica, o que se difere da inferência bayesiana, a qual não abordaremos aqui, pois pouco aparece em concurso.
Estatística, Estimador e Estimativa na Inferência
Anteriormente dissemos que um parâmetro é um número real desconhecido, porém constante.
Esse é um conceito muito importante. Além desse, podemos citar os conceitos de estatística, estimador e estimativa.
- Estatística é uma fução da amostra;
- Estimador é a estatística usada para estimar um parâmetro;
- Estimativa é um valor da estatística obtido de uma amostra particular.
Vamos exemplificar por meio da amplitude amostral. Considere a seguinte amostra:
![\[ x_1=3, x_2=7, x_3=4, x_4 = 0 \]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-65cd6901590750a5447b589396f66e17_l3.png "Rendered by QuickLaTeX.com")
Se tomarmos a estatística conhecida como amplitude amostral (estimador) para estimar o desvio padrão dos dados (parâmetro) temos:
![\[A = X_4-X_1\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-f31cbeb58c39c6facae41f972d40f783_l3.png "Rendered by QuickLaTeX.com")
Inicialmente, para obter a amplitude devemos calcular as estatísticas de ordem, por meio da ordenação do vetor.
![\[ X_{(1)} = 0, X_{(2)} =3, X_{(3)} = 4,X_{(4)} = 7\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-5e50cb72856806cd71a3997e1fb17edb_l3.png "Rendered by QuickLaTeX.com")
Como podemos ver acima trata-se da ordenação dos dados. Agora sabemos quem é o máximo e o mínimo valor da amostra:
![\[ X_{(\min)} = 0\ \mbox{ e } X_{(\max)} =7\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-f8f4f9d846782d98c94c535e6c8a45cf_l3.png "Rendered by QuickLaTeX.com")
Em resumo:
- Estatística:
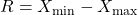, do ing. range; - Estimador: Amplitude Amostral
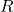; - Estimativa:
Se você não confundir esses conceitos, certamente está num ótimo caminho de apredizagem. É claro que o procedimento acima é apenas didático.
O Problema da Inferência
O principal problema da inferência estatística é a generalização de resultados a partir de uma pequena amostra.
Para isso o tamanho da amostra deve estar corretamente calculado. Partindo disso é importante saber qual estimador usar para estimar certo parâmetro.
Uma vez que já se sabe qual estimador usar, devemos conhecer bem as propriedades desse estimador.
Um bom estimador deve ser livre de viés, consistente e eficiente. Essas são propriedades desejáveis de um estimador.
O trabalho de um estatístico será estudar todas essas características a partir de uma amostra bem dimensionada.
A medida que conhece bem a estimação de parâmetros, o pesquisador poderá levantar hipóteses acerca de certos parâmetros.
Por fim chegamos nos chamados “teste de hipóteses”.
Inferência e Teste de Hipóteses Estatísticas
Um outro aspecto do problema da inferência será a realização de teste de hipóteses acerca dos parâmetros populacionais.
A verdade é que o estatístico sempre estará errando no seu trabalho, mas esse erro é controlado e gostaríamos de errar com um probabilidade bem pequena.
Certamente não queremos errar de propósito, mas o objeto de trabalho do pesquisador é o erro amostral. Esse sim é o que se pode controlar com a inferência estatística.
Nesse contexto é que estudamos os testes de hipóteses estatísticas. Uma hipótese é uma afirmação acerca de um parâmetro.
Por exemplo: considerando o modelo da binomial anterior, podemos admitir que
;
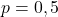
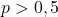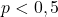
Da mesma forma vamos obter uma amostra para estudar essas hipóteses e chegar a conclusões por meio de técnicas de inferência.
Para isso vamos estabelecer uma hipótese padrão, a qual chamamos de hipóteses nula (
).
Em contraponto teremos a chamada hipótese alternativa, denotada por 
. Vamos realizar o seguinte confronto:
Aqui podemos incorrer em dois tipos de erro:
- Rejeitar a hipótese nula, quando na verdade ela é verdadeira; ou
- Não rejeitar a hipótese nula, dado que ela é falsa.
Na primeira situação estamos cometendo o erro do tipo I, enquanto no segundo caso, o erro do tipo II.
Se pudéssemos estabelecer uma probabilidade de cometer o erro do tipo I gostaríamos que fosse um valor bem pequeno.
Ao contrário, no erro do tipo II, o que importa é a probabilidade complementar, isto é, a probabilidade de rejeitar à 
, dado que ela é falsa.
Neste último caso temos uma probabilidade conhecida como poder do teste.
Quer aprender mais acerca de inferência? Conheça o curso Inferência Estatística Essencial para Concurso!
Conclusão
Como você viu, inferência é o assunto mais importante dentro da estatística e todas as demais matérias dentro dela apontam para a estatística indutiva.
Portanto a primeira conclusão é que dificilmente você deve começar estudando estatística por inferência.
Ao contrário, você precisará de boa base em probabilidade, e, por isso mesmo, uma dica importante é fazer um curso rápido nessa área.
Para isso você pode conhecer o curso Probabilidade Essencial para Concurso. Rápido e Prático.
Mesmo sabendo bem probabilidade, podemos colcluir ainda que sua preparação não prescinde de um curso direcionado somente para inferência estatística.
Juntar as peças do quebra-cabeça sozinho pode ser uma estratégia um pouco mais demorada. Ao invés disso, você pode agora ter o apoio de especialista em concurso de estatística.
Ingresse agora no curso Inferência Estatística Essencial para Concurso e começe a otimizar sua preparação.
Bons estudos!
Deixe um comentário