Veja a matemática essencial por trás dos segredos de probabilidade, estatística e ciência de dados

A probabilidade e a estatística são áreas fundamentais da ciência que desempenham um papel central em diversas disciplinas, como ciências sociais, biológicas, engenharia, economia e, mais recentemente, ciência de dados. Para entender esses campos, é importante dominar certos conceitos de matemática que servem de base para os principais teoremas e métodos utilizados. Neste artigo, vamos explorar a matemática essencial para quem deseja aprofundar-se em probabilidade e estatística.
Os melhores cursos de estatística para concurso:
- Matemática Essencial para Probabilidade e Estatística
- Probabilidade para Concurso
- Estatística para Concurso (Para Estatísticos e Cientistas de Dados)
Matemática Essencial: Álgebra
A álgebra é a linguagem básica da matemática, e sem ela é difícil lidar com a probabilidade e a estatística. Alguns tópicos-chave incluem:
- Manipulação de expressões algébricas: Simplificação de equações e fórmulas, fatoração, e solução de equações lineares e quadráticas.
- Funções: Compreender o comportamento de diferentes tipos de funções (lineares, quadráticas, exponenciais, etc.) é fundamental, pois muitos modelos estatísticos dependem de representações funcionais. Em estatística, as funções de probabilidade e densidade, como a função densidade da distribuição normal, são exemplos centrais.
- Resolução de equações: é essencial o uso de resoluções de equação como aquelas do primeiro e do segundo graus. Além disso é importante conhecer os conceitos de razão, proporção, dentre outros da matemática básica.
Cálculo
O cálculo é a base de matemática essencial para grande parte das técnicas avançadas de probabilidade e inferência estatística. Os dois principais tópicos do cálculo usados são:
- Derivadas: A derivada mede como uma função muda em relação às suas variáveis. Na probabilidade e estatística, isso é útil para maximizar funções de verossimilhança e encontrar pontos críticos em distribuições, além de se obter as funções de densidade em variáveis aleatórias contínuas.
- Integrais: As integrais são usadas para calcular áreas sob curvas, o que em probabilidade significa calcular probabilidades em distribuições contínuas, como a distribuição normal ou exponencial.
Por exemplo, a integral da função densidade de probabilidade de uma variável contínua entre dois pontos fornece a probabilidade da variável assumir valores dentro daquele intervalo.

Apesar de usarmos integrais para calcular probabilidade na distribuição normal, esses resultados estão em uma tabela frequentemente usada em provas de concursos.
Teoria dos Conjuntos
A teoria dos conjuntos é essencial para entender as operações de união, interseção e complemento de eventos em probabilidade. Elas são usadas para denotar a ocorrência de eventos e alguns conceitos importantes incluem:
- União e Interseção de Conjuntos: Na probabilidade, a união de dois eventos representa a ocorrência de pelo menos um deles, enquanto a interseção representa a ocorrência simultânea de ambos.
- Complemento de Conjuntos: O complemento de um evento é o conjunto de resultados que não pertencem ao evento. A probabilidade do complemento é frequentemente usada em problemas onde se calcula a chance de um evento não ocorrer. Veja abaixo alguns eventos e simbologia comumente adotada.
Veja abaixo uma tabela com algumas notações comuns:
| Propriedade | Notação |
| Evento certo de ocorrer | |
| Evento impossível de ocorrer | |
| Ocorrência simultânea dos eventos | |
| União de eventos | |
| Complementar (Não ocorrência do Evento | |
| Inclusão ( | |
| Não ocorrência simultânea |
Álgebra Linear
O conceito de vetores e matrizes da álgebra linear aparece com frequência em estatística, especialmente em análise multivariada e em modelos de regressão. O contexto multivariado é mais comum do que se pode imaginar nas aplicações de estatística e ciência de dados, dessa forma é importante dominar alguns conceitos chaves:
- Vetores e Matrizes: No contexto de modelos estatísticos, vetores podem representar conjuntos de dados ou coeficientes de variáveis, enquanto matrizes aparecem no cálculo de correlação, covariância, e na estimativa de parâmetros em modelos de regressão.
- Autovalores e Autovetores: Esses conceitos são usados em técnicas como Análise de Componentes Principais (PCA), que é uma ferramenta estatística amplamente utilizada para reduzir a dimensionalidade de conjuntos de dados grandes.
Conclusão
Para avançar em probabilidade e estatística, é necessário um sólido entendimento dos conceitos de matemática essencial que foram mencionados nesse artigo. Eles não apenas formam a base das fórmulas e métodos, mas também ajudam a desenvolver o raciocínio lógico e a resolução de problemas complexos. Seja para estudos acadêmicos ou aplicações em ciência de dados, dominar essas ferramentas é essencial para ter sucesso nessas áreas.
Lembre-se: a matemática é uma linguagem. Quanto mais fluente você for, mais claro será o entendimento dos problemas e soluções nas áreas de probabilidade e estatística.
Acesse agora o curso de Matemática Essencial para Probabilidade e Estatística!
Cursos rápidos e práticos para quem não é de exatas.


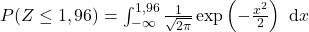




Deixe um comentário