Métodos de Estimação: Entenda as 3 Técnicas Mais Populares

Em estatística os métodos de estimação são os pilares da estatística inferencial. A ideia básica é usar informações da amostra para inferir resultados para a população. Antes de conhecermos a amostra podemos considerar que ela é completamente aleatória, de acordo com a técnica de amostragem com que é recolhida. Três métodos teóricos se destacam nessa seara: método dos momentos, método da máxima verossimilhança e estimação bayesiana.

O estatístico pode atuar no desenho amostral, na análise e planejamento de experimentos e conduzir estudos e pesquisas amostrais para garantir a tomada de decisão fundamentada em teoria e conhecimento nas evidências apontadas pelos dados disponíveis.

Aprenda calcular probabilidade na distribuição normal.

Conteúdo

1 Método da Máxima Verossimilhança
- 1.1 Vantagens
- 1.2 Desvantagens
2 Estimação pelo Método dos Momentos
- 2.1 Vantagens
- 2.2 Desvantagens
3 Estimação Bayesiana
- 3.1 Vantagens
4 Estimação em Concurso Público

Método da Máxima Verossimilhança

A Estimação por Máxima Verossimilhança (MLE – maximum likelihood estimator) é uma técnica poderosa e amplamente utilizada na inferência estatística. Este método busca os valores dos parâmetros que tornam a amostra observada a mais provável, maximizando a função de verossimilhança. A função de verossimilhança é construída a partir da distribuição de probabilidade dos dados, e os parâmetros estimados são aqueles que maximizam essa função.

Vantagens

Consistência: à medida que o tamanho da amostra aumenta, o estimador converge para o valor verdadeiro do parâmetro.
Eficiência: sob certas condições, os estimadores de MLE têm a menor variância possível.
Normalidade assintótica – quando o tamanho da amostra é sificientemente grande os MLE são aproximadamente normais.
Invariância – se queremos estimar um parâmetro 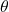$\theta$ , usamos o mesmo MLE para estimar uma função do parâmetro $g(\theta)$ .

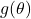A consistência nos garante que estamos acertando, em média, no parâmetro-alvo que se quer estimar, enquanto a eficiência garante uma variabilidade desejada em torno do verdadeiro valor do parâmetro. As propriedades desejadas de um estimador é que vão permitir avaliar o quão conveniente é este estimador. A média amostal, por exemplo, é um estimador não enviesado, eficiente e que segue uma distribuição normal, pelo teorema central do limite.

Desvantagens

Complexidade: a função de verossimilhança pode ser complexa e difícil de maximizar, especialmente em modelos com muitos parâmetros.
Dependência da Distribuição: a MLE assume que a forma da distribuição dos dados é conhecida.

Os métodos de estimação são importantes e devemos considerar as melhores propriedades para obter um bom estimador.

Estimação pelo Método dos Momentos

O Método dos Momentos é uma abordagem mais direta e intuitiva, que se baseia nos momentos amostrais (como média, variância, etc.) para estimar os parâmetros da população. A ideia é igualar os momentos teóricos de uma distribuição (momentos populacionais) aos momentos amostrais correspondentes.

Vantagens

Simplicidade: geralmente, é mais fácil de calcular do que a MLE.
Aplicabilidade: pode ser usado quando a MLE é impraticável.

Desvantagens

Menor Eficiência: os estimadores de momentos não são necessariamente eficientes, ou seja, podem não ter a menor variância possível.
Não é Ótimo: pode não aproveitar toda a informação disponível nos dados.

Exemplo: Para estimar a média $\mu$ e a variância $\sigma^2$ de uma distribuição, podemos igualar a média amostral $(\bar{x} \)$ e a variância amostral $s^2$ às respectivas expressões teóricas da média e variância da população.

Conheça os melhores cursos de estatística para concurso:

Estimação Bayesiana

A Estimação Bayesiana se difere das abordagens frequentistas (como MLE e Método dos Momentos) ao incorporar distribuições a priori sobre os parâmetros a serem estimados. Combina a distribuição a priori com a verossimilhança dos dados observados para formar a distribuição a posteriori dos parâmetros.

Vantagens

Flexibilidade: pode incorporar informações prévias e é aplicável a uma ampla gama de problemas.
Inferência Completa: fornece distribuições completas dos parâmetros, não apenas estimativas pontuais.

Desvantagens:

Complexidade Computacional: pode exigir técnicas avançadas de computação, como MCMC (Markov Chain Monte Carlo).
Dependência da Priori: os resultados podem ser sensíveis à escolha da distribuição a priori.

Exemplo: Se estamos estimando a média $\mu$ de uma população, podemos começar com uma distribuição a priori para $\mu$ , baseada em conhecimento prévio. A observação dos dados atualiza essa distribuição para a distribuição a posteriori, que reflete a nossa crença atualizada sobre o valor de $\mu$ .

Estimação em Concurso Público

Cada um desses métodos de estimação tem suas próprias vantagens e desvantagens, e a escolha do método adequado depende do contexto do problema, das características dos dados e das suposições que estamos dispostos a fazer. Seja maximizando a verossimilhança, igualando momentos ou incorporando informações prévias, a estimação é uma ferramenta fundamental para a inferência estatística e para a tomada de decisões baseada em dados.

Quando se trata de concurso público é importante conhecer e aplicar os métodos de estimação para as principais distribuições de dados conhecidas como distribuição normal, exponencial, binomial e poisson. Algumas vezes esses estimadores podem coincidir de acordo com o método aplicado.

Veja como esse assunto é cobrado em concurso: