Conteúdo
Introdução
Você sabe o que são quartis? Se você trabalha com dados, é provável que sim. Os quartis são uma medida estatística fundamental que nos ajuda a entender a distribuição dos nossos dados. Neste artigo, vamos explorar o que são os quartis, como calculá-los e por que são importantes.
Veja os melhores cursos de estatística para concurso:
- Probabilidade Essencial para Concursos
- Inferência Essencial para Concursos
- Teste de Hipóteses Essencial para Concursos
- Probabilidade Avançada para Concurso
- Estatística para Concurso (Para Estatísticos)
O que são quartis?
Os quartis são valores que dividem um conjunto de dados ordenados em quatro partes iguais. Eles são usados para entender a dispersão e a distribuição dos dados. Cada quartil representa uma porcentagem de dados, sendo o primeiro quartil (Q1) o valor que divide os 25% inferiores dos dados, o segundo quartil (Q2) divide os 50% medianos e o terceiro quartil (Q3) divide os 25% superiores.
Veja que ao saber o que é quartil, podemos rapidamente ter uma ideia da ordem dos dados.
Como calcular quartis?
Em estatística descritiva, os quartis são amplamente utilizados para entender a dispersão dos dados. Eles fornecem informações sobre a variação e a tendência central dos dados, sendo essenciais para análises estatísticas mais avançadas.
O primeiro passo para calcular quartis é ordenar o conjunto de dados: 
. A partir dos dados ordenados obtemos a mediana ou segundo quartil. Aqui há duas maneiras de efetuar o cálculo e para tanto devemos verificar o tamanho do conjunto de dados: se é par ou impar.
- Se
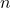é ímpar, o segundo quartil é a observação central do conjunto de dados;![\[Q_2=x_{\left(\frac{n+1}{2}\right)}\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-09c6da137f3ba682089b7c074c706d19_l3.png "Rendered by QuickLaTeX.com")
- Se 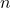é par, o segundo quartil é a média das duas observações centrais.
![\[Q_2=\frac{x_{\left(\frac{n}{2}\right)}+x_{\left(\frac{n}{2}+1\right)}}{2}\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-b4d053fd822ceedc59d23fda64bd19fa_l3.png "Rendered by QuickLaTeX.com")
Uma vez calculada a mediana teremos dois caminhos para obter os primeiro e segundo quartis.
O primeiro quartil é a mediana das observações abaixo de 
e o terceiro quartil é a mediana das observações superiores a .
Quartis em estatística
Em estatística descritiva, os quartis são amplamente utilizados para entender a dispersão dos dados. Eles fornecem informações sobre a variação e a tendência central dos dados, sendo essenciais para análises estatísticas mais avançadas.
Medidas de dispersão podem ser derivadas dos quartis dos dados utilizando diferentes abordagens. Aqui estão algumas medidas comuns de dispersão que podem ser calculadas a partir dos quartis:
- Amplitude interquartil (
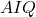): a amplitude interquartil é calculada como a diferença entre o terceiro quartil (
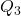) e o primeiro quartil (
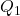). Matematicamente, 
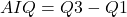. Ela fornece uma medida da dispersão dos dados, desconsiderando os valores extremos. - Desvio Quartílico: o desvio quartílico é metade da amplitude interquartil, ou seja,
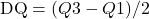. Esta medida é útil para entender a dispersão em torno da mediana. - Coeficiente de Variação Interquartil: é calculado como a amplitude interquartil dividida pela mediana e expressa como uma porcentagem, ou seja,
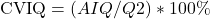. Esta medida padroniza a dispersão em relação à mediana, permitindo comparações entre diferentes conjuntos de dados.
Os quartis também nos informam acerca da simetria do conjuntos de dados.
Veja mais sobre quartis.
Interpretação dos quartis
A interpretação dos quartis depende do contexto dos dados. Em conjunto, eles nos dão uma ideia da dispersão e da simetria dos dados. Por exemplo, se os quartis estiverem muito próximos, os dados podem ser considerados mais simétricos.
Caso o conjunto de dados tenha outliers, ou valores atípicos, podem afetar significativamente os quartis. Se um conjunto de dados contiver outliers, os quartis podem não ser representativos da distribuição dos dados como um todo. Portanto, é importante considerá-los ao interpretar os quartis.
Todas essas observações acima nos mostram a importância de saber o que são quartis e sua correta interpretação.
Exemplo prático
Para melhor entender o que são os quartis vamos mostrar um exemplo prático de cálculo dessas métricas. Considere o seguinte conjunto de dados.
![\[3, 20, 16, 8, 10, 8, 13, 15, 7, 6\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-585d1eac61151270cf1f6bc37366eeec_l3.png "Rendered by QuickLaTeX.com")
Vamos mostrar a simbologia estatística estatística para os dados:
Passo 1: ordenação
Passo 2: cálculo da mediana: temo 
observações.
![\[Q_2=\frac{ x_{(10/2)}+x_{(10/2+1)}}{2}=\frac{x_{(5)}+x_{(6)}}{2}=\frac{8+10}{2}=9\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-6abd97fa606b39c799de57039a8adb01_l3.png "Rendered by QuickLaTeX.com")
Calculada a mediana temos o conjunto subdividido nas partes inferior e superior à mediana:
![\[\underbrace{3\ \ 6\ \ 7\ \ 8\ \ 8}_{\text{parte inferior}}\ \underbrace{10\ 13\ 15\ 16\ 20}_{\text{parte superior}}\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-5170e3b2d1c5ab3fce378ebdad4f1320_l3.png "Rendered by QuickLaTeX.com")
Passo 3: Mediana da parte inferior e mediana da parte superior
![\[\underbrace{3\ \ 6\ \ 7\ \ 8\ \ 8}_{\mathrm{med=7}}\ \underbrace{10\ 13\ 15\ 16\ 20}_{\mathrm{med}=15}\]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-147b4e949e8166afd2a4021f75e63a2b_l3.png "Rendered by QuickLaTeX.com")
Vemos que 
e 
. Assim vimos o que são quantis e como calcular essas métricas estatísticas.
Vimos o que são quartis veja abaixo uma questão envolvendo o conceito.
Deixe um comentário