
A prova da Polícia Federal de 2021 veio fora do padrão Cespe/Cebraspe. De fato, nem os mais bem preparados futuros PF esperavam nível tão acima na prova de estatística. Aqui você vê o gabarito extraoficial, de quebra ainda confere a resolução da prova passo a passo.
O nível acima da prova mais temida do concurso PF não tira o brilho do concurso, pois a dificuldade atinge a todos os candidatos, deixando todos em pé de igualdade na disputa.
Confira também:
- Como estudar estatística para a Polícia Federal
- Importância da Estatística: comece estudar agora
- 5 Técnicas de Estudo para ter 3x maisresultado em concurso
De antemão fica claro que as questões de estatística do concurso da Polícia Federal vão apenas ratificar o sucesso dos mais bem preparados para essa prova.
Por outro lado, decerto que trarão mais frustração para quem patinou em estatística.
Leia esse post até o final porque vale a pena pois você sairá daqui um pouco melhor na matéria mais temida da prova!
Conteúdo
Agente da Polícia Federal: Resolução de Estatística
Abaixo você confere a resolução do primeiro bloco da prova de agente da PF:
- Considerando que o horário de ocorrência de certo tipo de crime em determinado local seja representado por uma variável aleatória contínua
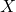 , cuja função de densidade é escrita como
, cuja função de densidade é escrita como ![Rendered by QuickLaTeX.com \[\[f(x)=\gamma(x-12)^2, \]](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-e830464cfaf2d029ae2e090566483ab2_l3.png)
em que ![]() e
e ![]() é uma constante de normalização (
é uma constante de normalização (![]() ), julgue os itens subsequentes.
), julgue os itens subsequentes.
37. ![]() .
.
38. O valor da constante ![]() é inferior a 0,01.
é inferior a 0,01.
39. O valor esperado de ![]() é igual a 12.
é igual a 12.
Como se trata de variável aleatória (v.a) contínua a probabilidade de ![]() assumir qualquer valor real é nula, por construção do conceito de função de distribuição:
assumir qualquer valor real é nula, por construção do conceito de função de distribuição: ![]() . Além disso, o valor de
. Além disso, o valor de ![]() deve ser positivo. Portanto o item 37. E (errado).
deve ser positivo. Portanto o item 37. E (errado).
Anteciadamente já se pode falar que essa questão veio de mão beijada. Já é manjada em provas Cespe.
A fim de resolver o item 38, considere a transformação: ![]() . Assim, devemos ter
. Assim, devemos ter ![]() . Para que essa função seja de densidade faça:
. Para que essa função seja de densidade faça:
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{-12}^{12}\gamma u^2\ \mathrm{d}u&=&1\\ \gamma \left(\frac{u^3}{3}\Big|_{-12}^{12}\right)&=&1\\ \gamma\left[\frac{12^3}{3}-\frac{(-12)^3}{3}\right]&=&1\\ 1152\gamma &=&1\\ \gamma=\frac{1}{1152}&<&0,001\end{eqnarray*}](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-8feb2a9f8ee4d566907dd94e88158fd4_l3.png)
Finalmente, chegamos à conclusão de que o item tem gabarito 38. C . Nota-se que a Cebraspe caprichou nas contas de estatística.
Com o objetivo de calcular o valor esperado de ![]() , vamos, de início, encontrar a média de
, vamos, de início, encontrar a média de ![]() . Por definição
. Por definição ![]() , mas será mais fácil resolver a integral em
, mas será mais fácil resolver a integral em ![]() .
.
![Rendered by QuickLaTeX.com \begin{eqnarray*}\hbox{E}(U)&=&\int_{-12}^{12} u \times \gamma u^2\ \mathrm{d}u\\ \hbox{E}(U)&=& \int_{-12}^{12}\gamma u^3\ \mathrm{d}u\\ \hbox{E}(U)&=&\gamma \left(\frac{u^4}{4}\Bigg|_{-12}^{12}\right)\\ \hbox{E}(U)&=&\gamma\left[\frac{12^4}{4}-\frac{(-12)^4}{4}\right]\\\hbox{E}(U)&=&0\end{eqnarray*}](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-694bb3bf41740c5476b63d72a173156a_l3.png)
Em conclusão, agora usamos as propriedades do valor médio para obter ![]() .
.
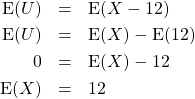
Apesar do disfarce, essa questão trouxe muitos conceitos de probabilidade, inclusive, o bom manejo de valor médio.
Veja a resolução:
Agente da PF: prova de estatística difícil
Quem achou que ingressar na PF seria moleza, ficou assustado com a prova de estatística. Ainda assim, prova difícil é boa para quem mais estudou correto.
Por isso mesmo é bom não se enganar e fazer um bom curso de probabilidade.
Daqui em diante vamos a resolver o segundo bloco da prova de agente da Polícia Federal, mas fique em paz porque você vai sair desse post com um melhor nível na sua jornada de concurso.
Enunciado Agente da PF
Considere que ![]() e
e ![]() sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade
sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade
![]()
na qual ![]() e
e ![]()
com base nessas afirmações , julgue os itens seguintes.
40. ![]() .
.
41. ![]() e
e ![]() são variáveis aleatórias independentes.
são variáveis aleatórias independentes.
42. ![]() é uma variável uniforme no intervalo
é uma variável uniforme no intervalo ![]() .
.
Em que pese não haver histórico de questões nesse nível em provas da Polícia Federal, o fato é que o conteúdo da Cespe é padrão.
Nesse sentido você pode esperar outras provas com esse elevado padrão em estatística.
Para começar a resolução deve-se, em princípio, ser calculadas as funções à margem para ![]() e
e ![]() .
.
Entretanto obtendo a densidade de ![]() já obtemos também para
já obtemos também para ![]() .
.
Resolução Estatística PF
Dessa forma, temos:
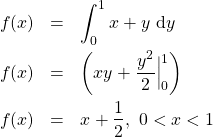
Por conseguinte ![]() . Deste ponto em diante já podemos tirar duas conclusões:
. Deste ponto em diante já podemos tirar duas conclusões:
- De começo,
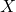 e
e 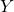 não são independentes pois,
não são independentes pois, 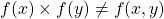 ;
; - Adicionalmente,
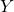 não segue a distribuição uniforme porque
não segue a distribuição uniforme porque 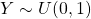 deve ter
deve ter 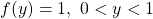 .
. - Resumo: os itens 41. E e 42. E.
Pode-se inferir facilmente ques os itens 41 e 42 estavam em nível de dificuldade mais fácil. Tudo bem, nem tanto, admito.
Por outro lado, para resolver o item 40 era bom conhecer o seguinte resultado.
![]()
Para finalizar esse bloco devemos calcular a esperança de ![]() , pontanto deve-se calcular a densidade condicional.
, pontanto deve-se calcular a densidade condicional.
![]()
Assim, o valor esperado dado que ![]() é dado por:
é dado por:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hbox{E}\left[Y|X\right]&=&y\times f(y|x)\ \mathrm{d}y\\ \hbox{E}\left[Y|X\right]&=&\int_0^1\frac{xy+y^2}{x+\frac{1}{2}} \\ \hbox{E}\left[Y|X\right]&=&\frac{1}{x+\frac{1}{2}}\int_0^2xy+y^2\ \mathrm{d} y \\ \hbox{E}\left[Y|X\right]&=&\frac{1}{x+\frac{1}{2}}\left[\frac{xy^2}{2}+\frac{y^3}{3}\Bigg|_0^1\right]\\ \hbox{E}\left[Y|X\right]&=&\frac{1}{x+\frac{1}{2}}\left(\frac{x}{2}+\frac{1}{3}\right)=\frac{1}{4}+\frac{1}{3}\\ \hbox{E}\left[Y|X=1/2\right]&=&\frac{7}{12}\end{eqnarray*}](https://estatisticaparaconcurso.com/wp-content/ql-cache/quicklatex.com-8275d519eeb26a40c9871e2a5398959f_l3.png)
Por fim, o resultado final é ![]() . Logo, temos o item 40. E.
. Logo, temos o item 40. E.
Essa questão foi acima do normal. De fato, aqui a Cebraspe pesou a mão, mas o bom aluno gostou desse exercício.
Exercícios desse tipo servem pra reforçar o sucesso daqueles alunos mais bem treinados. Por isso mesmo não desanime!
Ingresse agora no curso Estatística Polícia Federal.
Apesar da resolução acima, aqui você pode assistir à aula para ficar mais claro.
Enfim, qualquer dúvida, fico à sua disposição. Sei que as matéiras são difíceis, todavia estou aqui para ajudar você nessa missão.
A Questão mais difícil para Agente PF
A prova para Agente da Polícia Federal foi bem exigente com estatística inferencial, entretanto caprichou nos conceitos.

De fato, isso pode ser visto no próximo bloco de questões. Temos propriedade de estimador e métodos de estimação cobrados nesses itens.
De começo não se exije muita conta, mas sim compreensão da teoria.
Confira aqui o gabarito preliminar da prova do concurso PF 2021!
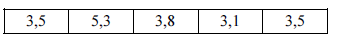
Considerando que o cojunto de dados apresentado represente uma realização da amostra aleatória simples de tamanho ![]() retirada de uma população
retirada de uma população ![]() , cuja função de probabilidade acumulada é escrita como
, cuja função de probabilidade acumulada é escrita como
![]()
Onde ![]() é o parâmetro desconhecido, julgue os itens que se seguem.
é o parâmetro desconhecido, julgue os itens que se seguem.
43. A média amostral é uma estatística suficiente para a estimação do parâmetro ![]() .
.
44. A estimativa de máxima verossimilhança para o parâmetro ![]() é igual ou superior a
é igual ou superior a ![]() .
.
45. Pelo método dos mínimos quadrados ordinários, a estimativa da média populacional é igual ou superior a ![]() .
.
Conceitos Importantes na Prova de Agente
Aqui vamos começar pela questão 44. O EMV é o valor de ![]() que dá a maior probabilidade de que a amostra observada ocorra.
que dá a maior probabilidade de que a amostra observada ocorra.
Em primeiro lugar, veja que ![]() , isto é,
, isto é, ![]() é sempre supeior ou igual à
é sempre supeior ou igual à ![]() para todo valor da amostra.
para todo valor da amostra.
Além disso, suponha que se possa calcular ![]() . Com isso pode-se avaliar qual
. Com isso pode-se avaliar qual ![]() nos dá a maior probabilidade da amostra observada ocorrer.
nos dá a maior probabilidade da amostra observada ocorrer.
Partindo disso, posso imaginar que ![]() seja a média amostral,
seja a média amostral, ![]() .
.
A média é dada pelo cálculo ![]() , portanto temos
, portanto temos
![]()
Em conclusão, podemos escrever:
![]()
Isso significa que a amostra ![]() não ocorreria, pois deve-se ter
não ocorreria, pois deve-se ter ![]() .
.
O resultado acima não é coerente pois na amostra ocorre os valores
![]()
O mesmo cálculo pode ser usado para concluir que o EMV não pode ser a mediana dos dados. Logo, parece viável admitir que o EMV é o mínimo da amostra.
Adicionalmente, o EMV não pode ser qualquer outra estatística de ordem, a não ser que se admita ser o mínimo o estimador que quero achar.
![]()
Conclui-se que ![]() é a estimativa correta. O gabarito 44. E.
é a estimativa correta. O gabarito 44. E.
Estimação por Mínimos Quadrados
Na questão 45 temos o clássico MQO, ademais, bastava saber que se trata da média da amostra.
Ainda assim vamos demostrar esse fato abaixo. Seja ![]() o valor médio.
o valor médio.
 é o erro que se comete ao considerar o valor médio
é o erro que se comete ao considerar o valor médio 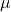 ;
;- Vamos minimizar a soma
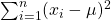 ;
;
Conquanto seja assustador, você deve chegar na prova sabendo desse resultado. Ao se realizar a amostra, agora temos uma função da média.
![]()
Com o objetivo de tornar mínima a soma, deriva-se em relação à ![]() :
:
![]()
Assim, ao fazer ![]() , temos:
, temos:
![]()
Nesse ínterim fica fácil, sabendo que se trata da média, concluir que a estimativa de MQO para a média da população é ![]() .
.
O Que é uma Estatística Suficiente: Breve Resumo
Antes de tudo, você deve saber que uma estatística é uma função da amostra.
A ideia é trocar
![]()
por uma função que pode ser:
- média;
- moda;
- mediana;
- mínimo,
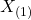 , o menor valor da amostra;
, o menor valor da amostra; - máximo,
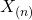 , maior valor da amostra; etc.
, maior valor da amostra; etc.
Contanto que se troque o vetor de dados por uma estatística de tal sorte que não se perca informação, conclui-se que esta é uma estatística suficiente.
Ademais, podemos ter mais de uma estatística dessa qualidade.
Visto que há redução dos dados, não podemos perder nenhuma informação da amostra em relação ao parâmetro sendo estimado.
Há alguns critérios técnicos para se determinar se uma estatística é suficiente, algo além do propósito aqui. Entretanto, parece razoável ver que se usarmos a média amostral vamos perder informação acerca de ![]() .
.
Em razão de ![]() ser estimado pelo mínimo da amostra, ao considerar a média, estmos a perder a “melhor” informação acerca do parâmetro
ser estimado pelo mínimo da amostra, ao considerar a média, estmos a perder a “melhor” informação acerca do parâmetro ![]() .
.
Em síntese, a média amostral não é uma estatística suficiente para estimar ![]() . Item 43. E.
. Item 43. E.
A ess altura você deve estar se perguntando como se preparar nesse nível? Conheça a Operação Estatística Polícia Federal! É também indicado pra você que vai fazer um concurso Fiscal!
De acordo com o programa da Cebraspe, suficiência está inserida na estimação pontual. Ainda que previsto, esse assunto é raro em concurso, diante disso, essa questão surpreendeu muitos concurseiros.
Em que pese ter alguns critérios técnicos para determinar se uma estatística é suficiente, de fato, o assunto é bem técnico e exige dose de abstração.
Você vai fazer CONCURSO FISCAL, veja probabilidade no seu próximo nível. PROBABILIDADE PARA CONCURSO.
.
Questões Cebraspe PF Mais Comuns
Esse bloco de quetões tem história de aparecer mais comumente nas provas Cespe, ainda assim não são questões bobas.
Desse modo exigiam atenção e bom conhecimento de regressão linear simples. Além disso, dominar a álgebra dos mínimos quadrados.
Um estudo objetivou avaliar a evolução do número mensal ![]() de milhares de ocorrências de certo tipo de crime em determinado ano. Com base no método dos mínimos quadrados ordinários, esse estudo apresentou um modelo de regressão linear simples da forma
de milhares de ocorrências de certo tipo de crime em determinado ano. Com base no método dos mínimos quadrados ordinários, esse estudo apresentou um modelo de regressão linear simples da forma
![]()
em que ![]() representa a reta ajustada em função da variável
representa a reta ajustada em função da variável
regressora ![]() , tal que
, tal que ![]() .
.
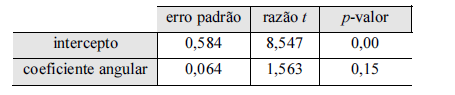
Os erros padrão das estimativas dos coeficientes desse modelo, as razões t e seus respectivos p-valores encontram-se na tabela a seguir.
Os desvios padrão amostrais das variáveis ![]() e
e ![]() foram,
foram,
respectivamente, 1 e 3,6.
Com base nessas informações, julgue os itens a seguir.
46. Se a média amostral da variável ![]() for igual a 6,5, então a
for igual a 6,5, então a
média amostral da variável será igual a 4,35 mil ocorrências.
47. Considere que ![]() denote o coeficiente angular do modelo de
denote o coeficiente angular do modelo de
regressão linear simples e considere, ainda, que o teste de hipóteses ![]() . Nessa situação, com referência a esse teste, caso o nível de significância escolhido seja igual a 5%, os resultados do estudo em questão indicarão que não há evidências estatísticas contra a hipótese nula
. Nessa situação, com referência a esse teste, caso o nível de significância escolhido seja igual a 5%, os resultados do estudo em questão indicarão que não há evidências estatísticas contra a hipótese nula ![]() .
.
48. A correlação linear entre as variáveis e ![]() e
e ![]() foi igual a
foi igual a ![]() .
.
Resolução Regressão Linear
Primeiro de tudo, regressão linear é muito comum em provas Cespe. Além disso as questões da Polícia Federal foram bem tranquilas.
Em síntese, tivemos direta aplicação de fórmula. Assim, a banca não fugiu muito do seu modo de cobrar regressão.
Temos o modelo ![]() . Usando o método MQO, estimamos o coeficiente
. Usando o método MQO, estimamos o coeficiente ![]() pela fórmula
pela fórmula
![]()
Com isso, partindo desse resultado, podemos concluir que
![]()
Em conclusão o item 46. C está correto, portanto um exercício bem fácil.
Teste de Hipóteses Clássico
O conteúdo de regressão traz uma parte clássica acerca da inferência dobre os coeficientes do modelo. Todavia a Cebraspe deu todos os dados de mão beijada.
i) Queremos testar:
![]()
ii) A estatística de teste é a razão ![]() .
.
iii) Apesar de fornecido o valor acima, não vamos precisar consultar uma tabela ![]() porque foi dado o p-valor.
porque foi dado o p-valor.
iv) Decisão: como o p-valor para o coeficiente angular foi igual a 0,15, isto é, ![]() , esse seria o menor nível de significância para o qual rejeitaríamos a hipóteses nula. Portanto NÃO há evidência contra
, esse seria o menor nível de significância para o qual rejeitaríamos a hipóteses nula. Portanto NÃO há evidência contra ![]() .
.
Conclui-se que o item 47. C. Veja que não há evidência contra a hipótese de que ![]() , assim podemos dizer que há contra o modelo.
, assim podemos dizer que há contra o modelo.
Cáculo do Coeficiente de Correlação
Para o cálculo da correlação lembre de algumas fórmulas úteis, mas para não ficar apenas nas fórmulas puras, veja que:
![]()
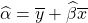 ;
;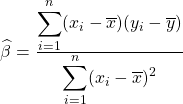
- Seja
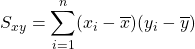 ;
; 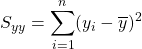 e
e 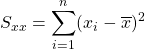
- Note que
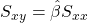 e
e 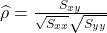
Por fim, tem-se que ![]() , logo
, logo ![]() .
.
No vídeo acima você vê a solução, entretanto eu erreu na conclusão do teste de hipóteses. Houve confusão entre evidência contra ![]() , que não há, e contra o modelo.
, que não há, e contra o modelo.
Apesar desse erro a resolução estácorreta, inclusive com a conclusão por não rejeição da hipótese nula.
Gabarito Oficial Preliminar Polícia Federal
O Cebraspe divulgou os gabaritos oficiais, mas o acesso está restrito aos candidatos em http://www.cebraspe.org.br.
Dica extra: acompanhe o canal de estatística para concurso: http://www.youtube.com/c/concurseiroestatistico
Baixe mais provas da Polícia Federal e estatística e ciência de dados para concurso.







Deixe um comentário